[자료구조] 1. 검색 알고리즘(선형검색, 이진검색, 해시법)

개발/자료구조

[자료구조] 1. 검색 알고리즘(선형검색, 이진검색, 해시법)

hongtaekki 2022. 1. 11. 21:47

1. 선형 검색

1.1. 개념

직선 모양(선형)으로 늘어선 배열에서 검색하는 경우에 원하는 키값을 가진 원소를 찾을 때까지 맨 앞부터 스캔하여 순서대로 검색하는 알고리즘

1.2. 종료조건

검색할 값을 찾지 못하는 배열의 맨 끝을 지나간 경우 - 검색 실패
검색할 값과 같은 원소를 찾는 경우 - 검색 성공

1.3. 구현코드

from typing import Any, Sequence


def seq_search(a: Sequence, key: Any) -> int:
    i = 0

    while True:
        if i == len(a):
            return -1       # 검색에 실패하여 -1을 반환
        if a[i] == key:
            return i        # 검색에 성공하여 현재 검사한 배열의 인덱스를 반환
        i += 1


if __name__ == '__main__':
    num = int(input('원소 수를 입력하세요: '))      # num값을 입력받는다
    x = [None] * num                            # 원소 수가 num인 배열을 생성

    for i in range(num):
        x[i] = int(input(f'x[{i}]: '))

    ky = int(input('검색할 값을 입력하세요.: '))      # 검색할 키 ky를 입력받음

    idx = seq_search(x, ky)                       # ky와 값이 같은 원소를 x에서 검색

    if idx == -1:
        print('검색값을 갖는 원소가 존재하지 않습니다.')
    else:
        print(f'검색값은 x[{idx}]에 있습니다.')

2. 이진 검색

2.1. 개념

원소가 오름차순이나 내림차순으로 정렬된 배열에서 좀 더 효율적으로 검색할 수 있는 알고리즘

2.2. 검색방법

예시) 오름차순으로 정렬된 배열에서 '39'를 검색하자.

(1) 배열의 중앙에 위치한 원소 a[5]인 31에 주목

(2) 찾아야할 값 39는 31보다 뒤쪽에 존재하기 때문에 검색 대상을 a[6] ~ a[10]으로 좁힐 수 있다.

(3) 업데이트된 대상 범위의 중앙 원소인 a[8]인 68에 주목한다. 39가 중앙 원소인 68보다 앞쪽에 존재하므로 검색 대상을 a[6] ~ a[7]로 좁힐 수 있다.

(4) 검색할 대상이 2개 남았다. 다시 중앙 원소로 앞쪽에 39를 주목한다.
(인덱스 6과 7의 중앙값은 (6+7) // 2로 계산하여 소수점 이하 버리고 6이 된다)

(5) 39는 찾아야 할 키의 값과 일치하므로 검색하는 데 성공한다.

2.3. 구현코드

from typing import Any, Sequence

def bin_search(a : Sequence, key:Any) -> int :
    pl = 0              # 검색 범위 맨 앞 원소의 인덱스
    pr = len(a) - 1     # 검색 범위 맨 끝 원소의 인덱스

    while True:
        pc = (pl + pr) // 2     # 중앙 원소의 인덱스

        if a[pc] == key:        
            return pc           # 검색 성공
        elif a[pc] < key:       
            pl = pc + 1         # 검색 범위를 뒤쪽 절반으로 좁힘
        elif a[pc] > key:
            pr = pc + 1         # 검색 범위를 앞쪽 절반으로 좁힘
        if pl > pr:
            break               # 검색 실패
    return -1

if __name__=='__main__':
    num = int(input('원소 수를 입력하세요 : '))
    x = [None] * num            # 원소 수가 num인 배열을 생성

    print('배열 데이터를 오름차순으로 입력하세요.')

    x[0] = int(input('x[0]: '))

    for i in range(1, num):
        while True:
            x[i] = int(input(f'x[{i}]: '))
            if x[i] >= x[i - 1]:                    # 바로 직전에 입력한 원솟값보다 큰 값을 입력
                break

    ky = int(input('검색할 값을 입력하세요. : '))       # 검색할 키값 ky를 입력

    idx = bin_search(x, ky)                         # ky와 같은 원소를 x에서 검색

    if idx == -1:
        print('검색값을 갖는 원소가 존재하지 않습니다.')
    else:
        print(f'검색값은 x[{idx}]에 있습니다.')

3. 복잡도

3.1. 개념

프로그램의 실행 속도(또는 실행하는 데 필요한 시간)는 프로그램이 동작하는 하드웨어나 컴파일러 등의 조건에 따라 달라진다.
알고리즘의 성능을 객관적으로 평가하는 기준을 복잡도라고 한다.

3.2. 종류

시간 복잡도(time complexity) : 실행하는 데 필요한 시간을 평가한다.
공간 복잡도(space complexity) : 메모리(기억 공간)와 파일 공간이 얼마나 필요한지를 평가한다

4. 해시법

4.1. 개념

'데이터의 저장할 위치 = 인덱스'를 간단한 연산으로 구하는 것을 말한다. 이 방법은 원소의 검색뿐 아니라 추가, 삭제도 효율적으로 수행할 수 있다.

4.2. 방식

배열의 키(원소의 값)를 원소 개수인 13으로 나눈 나머지를 표에 정리한 것이다. 이 값을 해시값이라고 하고 데이터에 접근할 때 기준이 된다.

새로만든 [a]에 35를 추가해보자. 35를 13으로 나눈 나머지는 9이므로 그림 [b]처럼 x[9]에 저장한다. 데이터를 추가해도 원소를 이동할 필요가 없어진다.

4.3. 해시충돌

해시충돌
- 18을 추가한다고 생각해보자. 18을 13으로 나눈 나머지가 5이므로 저장할 곳은 x[5]이지만, 이곳에는 이미 값이 들어 있다. 이처럼 저장할 곳이 중복되는 현상을 충돌이라고 한다.

결방법(1) - 체인법

충돌이 발생했을 때 재해시를 수행하여 빈 버킷을 찾는 방법을 말하며 닫힌 해시법이라고도 한다.
체인법에서는 해시값이 같은 데이터를 연결 리스트에 의해 체인 모양으로 연결한다.
배열의 각 버킷(해시 테이블)에 저장하는 것은 인덱스를 해시값으로 하는 연결 리스트의 앞쪽 노드를 참조하는 것이다.
구현코드

from __future__ import annotations
from typing import Any, Type
import hashlib

class Node:
    """해시를 구성하는 노드"""

    def __init__(self, key: Any, value: Any, next: Node) -> None:
        """초기화"""
        self.key   = key    # 키
        self.value = value  # 값
        self.next  = next   # 뒤쪽 노드를 참조

# Do it! 실습 3-5 [B]
class ChainedHash:
    """체인법을 해시 클래스 구현"""

    def __init__(self, capacity: int) -> None:
        """초기화"""
        self.capacity = capacity             # 해시 테이블의 크기를 지정
        self.table = [None] * self.capacity  # 해시 테이블(리스트)을 선언

    def hash_value(self, key: Any) -> int:
        """해시값을 구함"""
        if isinstance(key, int):
            return key % self.capacity
        return(int(hashlib.sha256(str(key).encode()).hexdigest(), 16) % self.capacity)

# Do it! 실습 3-5[C]
    def search(self, key: Any) -> Any:
        """키가 key인 원소를 검색하여 값을 반환"""
        hash = self.hash_value(key)  # 검색하는 키의 해시값
        p = self.table[hash]         # 노드를 노드

        while p is not None:
            if p.key == key:
                 return p.value  # 검색 성공
            p = p.next           # 뒤쪽 노드를 주목

        return None              # 검색 실패

    def add(self, key: Any, value: Any) -> bool:
        """키가 key이고 값이 value인 원소를 삽입"""
        hash = self.hash_value(key)  # 삽입하는 키의 해시값
        p = self.table[hash]         # 주목하는 노드

        while p is not None:
            if p.key == key:
                return False         # 삽입 실패
            p = p.next               # 뒤쪽 노드에 주목

        temp = Node(key, value, self.table[hash])
        self.table[hash] = temp      # 노드를 삽입
        return True                  # 삽입 성공

# Do it! 실습 3-5[D]
    def remove(self, key: Any) -> bool:
        """키가 key인 원소를 삭제"""
        hash = self.hash_value(key)  # 삭제할 키의 해시값
        p = self.table[hash]         # 주목하고 있는 노드
        pp = None                    # 바로 앞 주목 노드

        while p is not None:
            if p.key == key:  # key를 발견하면 아래를 실행
                if pp is None:
                    self.table[hash] = p.next
                else:
                    pp.next = p.next
                return True  # key 삭제 성공
            pp = p
            p = p.next       # 뒤쪽 노드에 주목
        return False         # 삭제 실패(key가 존재하지 않음)

    def dump(self) -> None:
        """해시 테이블을 덤프"""
        for i in range(self.capacity):
            p = self.table[i]
            print(i, end='')
            while p is not None:
                print(f'  → {p.key} ({p.value})', end='')  # 해시 테이블에 있는 키와 값을 출력
                p = p.next
            print()

해결방법(2) - 오픈주소법

충돌이 발생했을 때 재해시를 수행하여 빈 버킷을 찾는 방법을 말하며 닫힌 해시법이라고도 한다.
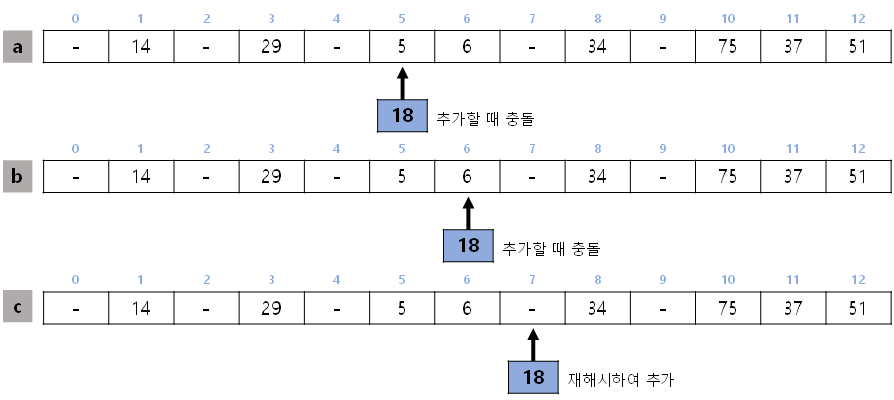
[a]에서 해시의 충돌이 발생합니다. 이럴 때 재해시를 수행하는데, 키에 1을 더하여 13으로 나눈 나머지를 사용했다.
(18+1) % 13으로 나머지 6을 얻는다. b처럼 인덱스 6인 버킷도 값이 존재하므로 재해시를 수행
(19+1) % 13을 통해 7을 얻으면 인덱스가 7인 버킷에 18을 추가한다.

구현코드

from __future__ import annotations
from typing import Any, Type
from enum import Enum
import hashlib

# 버킷의 속성
class Status(Enum):
    OCCUPIED = 0  # 데이터를 저장
    EMPTY = 1     # 비어 있음
    DELETED = 2   # 삭제 완료

class Bucket:
    """해시를 구성하는 버킷"""

    def __init__(self, key: Any = None, value: Any = None,
                       stat: Status = Status.EMPTY) -> None:
        """초기화"""
        self.key = key      # 키
        self.value = value  # 값
        self.stat = stat    # 속성

    def set(self, key: Any, value: Any, stat: Status) -> None:
        """모든 필드에 값을 설정"""
        self.key = key      # 키
        self.value = value  # 값
        self.stat = stat    # 속성

    def set_status(self, stat: Status) -> None:
        """속성을 설정"""
        self.stat = stat

class OpenHash:
    """오픈 주소법을 구현하는 해시 클래스"""

    def __init__(self, capacity: int) -> None:
        """초기화"""
        self.capacity = capacity                 # 해시 테이블의 크기를 지정
        self.table = [Bucket()] * self.capacity  # 해시 테이블

    def hash_value(self, key: Any) -> int:
        """해시값을 구함"""
        if isinstance(key, int):
            return key % self.capacity
        return(int(hashlib.md5(str(key).encode()).hexdigest(), 16)
                % self.capacity)

    def rehash_value(self, key: Any) -> int:
        """재해시값을 구함"""
        return(self.hash_value(key) + 1) % self.capacity

    def search_node(self, key: Any) -> Any:
        """키가 key인 버킷을 검색"""
        hash = self.hash_value(key)  # 검색하는 키의 해시값
        p = self.table[hash]         # 버킷을 주목

        for i in range(self.capacity):
            if p.stat == Status.EMPTY:
                break
            elif p.stat == Status.OCCUPIED and p.key == key:
                return p
            hash = self.rehash_value(hash)  # 재해시
            p = self.table[hash]
        return None

    def search(self, key: Any) -> Any:
        """키가 key인 갖는 원소를 검색하여 값을 반환"""
        p = self.search_node(key)
        if p is not None:
            return p.value  # 검색 성공
        else:
            return None     # 검색 실패

    def add(self, key: Any, value: Any) -> bool:
        """키가 key이고 값이 value인 요소를 추가"""
        if self.search(key) is not None:
            return False             # 이미 등록된 키

        hash = self.hash_value(key)  # 추가하는 키의 해시값
        p = self.table[hash]         # 버킷을 주목
        for i in range(self.capacity):
            if p.stat == Status.EMPTY or p.stat == Status.DELETED:
                self.table[hash] = Bucket(key, value, Status.OCCUPIED)
                return True
            hash = self.rehash_value(hash)  # 재해시
            p = self.table[hash]
        return False                        # 해시 테이블이 가득 참

    def remove(self, key: Any) -> int:
        """키가 key인 갖는 요소를 삭제"""
        p = self.search_node(key)  # 버킷을 주목
        if p is None:
            return False           # 이 키는 등록되어 있지 않음
        p.set_status(Status.DELETED)
        return True

    def dump(self) -> None:
        """해시 테이블을 덤프"""
        for i in range(self.capacity):
            print(f'{i:2} ', end='')
            if self.table[i].stat == Status.OCCUPIED:
                print(f'{self.table[i].key} ({self.table[i].value})')
            elif self.table[i].stat == Status.EMPTY:
                print('-- 미등록 --')
            elif self.table[i] .stat == Status.DELETED:
                print('-- 삭제 완료 --')

저작자표시 비영리 변경금지 (새창열림)